Принято выделять несколько основных версий обнаружения великим итальянским средневековым математиком числового ряда, ставшего легендарным. Так, например, по одной из них, Фибоначчи посетил Египет. Там он достаточно много времени занимался изучением архитектуры здешней древней цивилизации. Местные пирамиды возводились именно с соблюдением пропорций «Золотого сечения». Возможно, именно этот факт и заставил Фибоначчи посвятить изучению данного понятия столь много времени.
Еще одной распространенной версией создания числовой последовательности Фибоначчи является решение банальной задачи для детей про зайчиков. Её условия были весьма простыми: «Сколько именно пар зайчиков можно получить за 1 год от пары зайчиков, если ежемесячно каждая пара зайчиков приносит по одной паре зайчиков ежемесячно, начиная со второго месяца».
В процессе нехитрых размышлений можно прийти к выводу, что первые 2 месяца продолжает оставаться одна пара зайчиков, на 3-ий месяц она уже приносит потомство. В результате становится 2 пары. На 4-ый месяц в увеличении потомства принимает участие все еще только одна пара, приносящая еще 1 пару зайчиков. Теперь их становится три пары. С 5-го месяца еще 1 пара начинает размножаться. В итоге число зайчиков растет на 2 пары и их становится 5 и так до 12 месяца или бесконености. Решение рассмотренной задачки позволяет получить такую последовательность чисел:
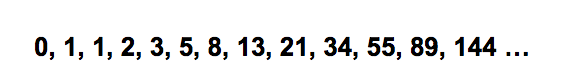
Данный ряд чисел на сегодняшний момент широко известен под названием «Числовая последовательность Фибоначчи». Настоятельно рекомендуем записать его и постараться запомнить наизусть, поскольку он обязательно пригодится в будущем для выполнения анализа рыночной ситуации. Особенность рассматриваемой последовательности можно сформулировать таким образом - ее каждое следующее число формируется посредством суммирования двух прошлых чисел, то есть перед нами естественная математическая универсальность действий. Весьма примечательным фактом в процессе изучения последовательности чисел Фибоначчи стало то, что каждые два соседствующих числа соотносятся между собой только в пропорции «Золотого сечения». Чтобы в этом убедиться, предлагаем наглядный пример:
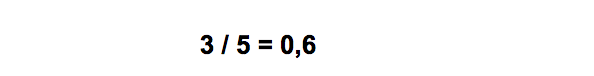
В этой ситуации можно увидеть пропорцию, которая практически полностью равняется «Золотому сечению» (0,618). Если же поменять указанные выше числа, то получится:
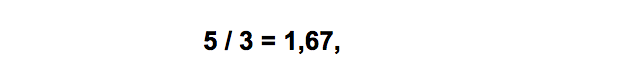
то есть, можно увидеть обратное отношение чисел последовательности, которое стремится к 1,618. Аналогичная ситуация наблюдается и в первом случае. Интересно, что связь с «Золотым сечением» значительно больше проявляется с ростом порядка чисел. Пропорция «Золотого сечения» прекрасно заметна при соотношении чисел, которые соседствуют в числовой последовательности Фибоначчи. Однако более интересный эффект заключается в том, что при соотношении чисел через каждое следующее подобная ситуация сохраняется. К примеру:

На основании представленной информации можно прийти к достаточно простому выводу, что Фибоначчи посредством несложных математических действий сумел открыть математическую прогрессию, имеющую максимально простой и универсальный алгоритм формирования. Плюс ко всему в ней всегда отображается уникальная «природная» пропорция «Золотого сечения», подтверждая тем самым ее «естественность» и универсальность.